Gavin R. Putland, BE PhD
| Saturday, October 08, 2016 | (Comment) |
Εὕρηκα 4th–8th October 2016: The observation by Huygens that should have discredited Newton's ‘rule’ for the extraordinary refraction of calcite
Huygens, in the fifth and longest chapter of his Treatise on Light (1690), explained the double refraction of “Iceland crystal” (transparent calcite) on the correct hypothesis that the secondary waves generated when the incident waves strike the crystal are spherical for the “ordinary” refraction (which satisfies Snell's law) and spheroidal for the “extraordinary” refraction (which does not).
With this theory, Huygens explained his observation that when a calcite crystal is placed on a horizontal page of text, the ordinary image of the text is raised higher than the extraordinary image, and that when the observer's head is rotated about a vertical axis, the height of the extraordinary image oscillates at twice the frequency of rotation — although Huygens' theory gave the height for only two (perpendicular) orientations of the observer's head [1, pp. 81–86]. Huygens died in 1695.
The first edition of Newton's Opticks (1704) did not deal with double refraction. But in Query 17 of the Latin edition (1706), which became Query 25 of later English editions (1717, 1721, 1730), Newton stated a ‘rule’ purporting to give the direction of the extraordinary ray in terms of that of the ordinary ray [2, p.356]. Consider two opposite, parallel faces of a calcite crystal (Fig. 1). Let a ray from an external point L strike one face at point P, and be refracted to point O on the opposite face by the Ordinary refraction, and to point E on the opposite face by the Extraordinary refraction. According to Newton's rule, the displacement OE, which I shall call the aberration, is the same, in both magnitude and direction, for all incident rays LP (provided of course that the internal ray is not intercepted by other faces of the crystal). Newton gave no justification for his rule, and made “no known attempt to deduce it from any principles of optics, corpuscular or otherwise” [3, p.327].
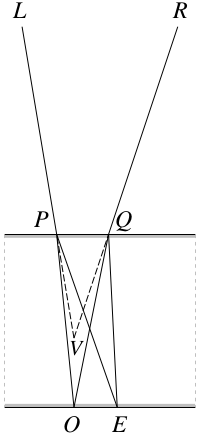
Fig. 1.
Now let us reverse the rays and the order in which the points (in Fig. 1) are defined. Let O be a point on the bottom face of the crystal. Let L be the observation point above the crystal, and let P be the point on the top face such that OPL is an ordinary refraction. Then let E be the point on the bottom face such that EPL is an extraordinary refraction. Hence OE is the aberration for PL. Let R be another observation point, and let Q be the point on the top face such that OQR is an ordinary refraction. Then, according to Newton's rule, OE is also the aberration for QR, so that EQR is an extraordinary refraction. Thus Newton's rule implies that if the ordinary image of O and the extraordinary image of E are in the same line of sight for one observation point, they are also in the same line of sight for any other observation point.
This implication came to the attention of the French mineralogist René Just Haüy. In an experiment published in 1788, Haüy found the distance between two points on a horizontal surface such that, if a calcite crystal was placed over them with the appropriate orientation, the ordinary image of one point coincided with the extraordinary image of the other. Then, if Newton's rule was correct, the coincident images would remain coincident as Haüy moved his eye. They didn't, so it wasn't! Haüy only considered movements in the principal section [3, pp. 335–6], i.e. the plane through OE and normal to the top and bottom faces; but that was enough.
In the light of his other experiments and their then-unknown imperfections [3, pp. 336–9], Haüy was led to propose a modification of Newton's rule, so that the aberration would be constant if measured in a plane through O sloping 30° upward towards E. Haüy's rule was only for a principal section. In the abstract of his paper in the Mémoires de l'Académie royale des Sciences, Haüy wrote: “I propose to prove in this memoir that the observations... give results that differ sensibly in several respects from those particular to Newton, and are closer to those of Huygens.” In the table of contents, the editor changed this to: “M'sieur Haüy has proposed in this memoir to analyze this phenomenon with a new precision, and this analysis leads to the same result as Newton”! (Quoted by Shapiro [4, p.257]; translated with the help of Google.)
As far as Newton's rule was concerned, there was nothing to gain by questioning the accuracy of Haüy's quantitative measurements, because Haüy had devised an experiment that sought only a qualitative effect. But, remarkably, he didn't need to take even that much trouble. If the ordinary image of one point and the extraordinary image of another had remained coincident as the observation point moved from side to side, that would have meant that the two images were at the same height, contrary to Huygens' observation!
Indeed, as the foregoing argument applies to all L and R, let L (in Fig. 1) be the pivot of the observer's Left eye and R the pivot of the observer's Right eye. Let the lines LP and RQ, when produced, intersect at point V — or if they don't intersect, let the observer compensate by going slightly hyper/hypotropic (“vertically cross-eyed”) so that they appear to intersect at point V. (By symmetry, for the ordinary refraction, no such compensation is necessary if (i) the plane LRO is normal to the top face or (ii) the segment LR is parallel to the top face and its perpendicular-bisector plane passes through O [note corrected 4th July 2017].) Then V is the (Virtual) ordinary image of O seen stereoscopically by both eyes. By construction, if Newton's rule is correct, V is also the (virtual) extraordinary image of E seen stereoscopically by both eyes, so that the two images, being coincident, are the same distance from the plane OE, i.e. at the same height if that plane is horizontal. But, as Huygens observed, they are not. “For one sees the letters and the paper on which they are written, as on two different stages at the same time...” [1, p.81].
Thus Huygens' observation — even if it is taken only qualitatively, and even if one ignores the additional information about the variation in height as the crystal (or the observer's head) is rotated — is enough to disprove Newton's rule.
(Considering my time constraints, I leave it to others to work out the extent to which the rules of Haüy and La Hire [3, p.333] can be reconciled with Huygens' observations of the height of the extraordinary image. La Hire, in 1710, proposed that the extraordinary refraction satisfied Snell's law except that the angles were measured with respect to the undeviated ray while the refractive index was less than for the ordinary refraction: 3/2 instead of 5/3.)
From the qualitative, let us proceed to the intuitive. For a natural face of the crystal, the extraordinary refraction is, let us say, biased in the sense that if the angle of incidence is zero, the angle of refraction is not, and vice versa. But for external rays close to the normal, the ordinary refraction is stronger in the sense that, for a given change in direction of the internal ray, there is a greater change in the direction of the external ray. When the crystal is placed on a horizontal page of text, the stronger ordinary refraction causes the ordinary image to be raised higher than the extraordinary image. Meanwhile the bias of the extraordinary refraction, although substantial, applies to both eyes and largely cancels out. Hence, although the height of the extraordinary image varies somewhat as the crystal is rotated, it remains below that of the ordinary image. In this conceptual framework, Newton's rule has the obvious defect that it does not allow for the lesser strength of the extraordinary refraction: it only allows for the bias!
(I note in passing that La Hire's rule obviously makes some allowance for both the lesser strength and the bias. Haüy's allowance for the lesser strength is not so obvious, at least to me, but Buchwald's graph [3, p.364] suggests that it outperforms both Newton and La Hire in the principal section.)
So, whether the argument is rigorous or intuitive, I am led to the embarrassing conclusion that when Newton's rule for the extraordinary refraction of calcite was first published, it was demonstrably inconsistent with the simplest and most readily reproducible of Huygens' original observations on double refraction.* But apparently nobody noticed. And while I stand ready to be corrected, I am not aware of Huygens getting any credit for this fact until now.
P.S. (10th October 2016)
I thank F.J. Dijksterhuis (author of [5]) for directing me to Huygens' notes from 1672/3 on the “Wonderful double refraction of Iceland crystal”, which show that I have undersold Huygens (but not necessarily oversold myself).
In these notes [6], Huygens proposed rules for the principal section and what I shall call the transverse section, i.e. the plane normal to both the surface and the principal section. Each rule is equivalent to Newton's except that the position of the point that I have called O (from which the aberration is measured) is calculated with a refractive index of just under 8/5 for the principal section, and about 300/217 for the transverse section, both indices being less than that for the ordinary refraction. Each index, being a ratio of sines, is only an approximation to what Huygens eventually called the “proportion of the refraction” for the relevant plane [1, pp. 70,80]; to make the approximation exact, the sine of the angle of refraction (inside the crystal) must be replaced by a sort of elliptical sine defined with respect to conjugate semi-axes of the appropriate elliptical cross-section of the spheroid. Thus, in the course of his inquiries, Huygens considered and rejected a theory of which Newton's later rule was a degenerate case, applied too widely.
In his Treatise, Huygens used his “proportions” and the ordinary index to explain the heights of the extraordinary image when viewed in the principal and transverse sections, and why they were less than the height of the ordinary image [1, pp. 81–86]. So Huygens certainly knew, no later than the drafting of his Treatise (1678), and possibly as early as 1672/3, that three proportions were needed to explain the heights of the images, and that therefore a rule with only one proportion, such as the one subsequently offered by Newton, would not suffice. Had he lived to see Newton's effort, he would have disposed of it in short order.
But my original point, which I have still not seen elsewhere, is that a single, qualitative observation of the different heights of the ordinary and extraordinary images was enough to sink Newton's rule.
Appendix (15th October 2016): Translation of the relevant sections of Huygens' Oeuvres complètes [6]
[Page numbers (at the top of each page), references to figures or margins, and my comments and citations are in square brackets. Footnotes (in French) are not included but are occasionally acknowledged in my comments. Knowing little Greek and no Latin, I have used Google Translate or, if that failed, William Whitaker's Words. Presumably the result is amateurish (except the last paragraph). I am willing to link to a better translation as soon as one appears.]

Fig. 132.
§ 3. Line AB [Fig. 132] bisects the obtuse angle of the upper face [that face being perpendicular to the plane of the diagram]. CDE, perpendicular to AB, represents a section or cross-plane, perpendicular to the upper face and also to the line AB.
GH is another plane parallel to CD, and so placed that the perpendicular GH is refracted into HE by the anomalous refraction. This causes any oblique ray in the plane GH to be refracted in the plane HE [which, like the plane KL, is perpendicular to the plane of the diagram, according to footnote 1].
The ray KLE, which is parallel to the oblique edge [according to Bartholinus, but not according to Huygens' later measurement], penetrates unrefracted straight to LE. But other rays in the same plane KL [perpendicular to the plane of the diagram] and oblique to the aforesaid ray KL are refracted not in the plane LE, but further inward towards LS, the [plane of the] refracted perpendicular, as they become more oblique to ray KL. [Cf. [5, p.147].]
The object E appears to the eye at K from the [ordinary] refraction at M.
§ 4. See the figure below [Fig. 133]. Line DE bisects the obtuse angle of the upper face [that face being perpendicular to the plane of the diagram]. Line AB is perpendicular to the plane thereof [the upper face]. BC is the anomalous refraction of this perpendicular. FBC, the angle of refraction of perpendicular rays, is a little less than 7 degrees when measured by the sun's rays. TTC is the ray that passes without refraction, parallel to the edges [according to Bartholinus].

Fig. 133.
[p. 411, approx.]
BF is the thickness of the crystal. DS is to DF as LO to LF and EV to EF, so that if the rays DD, LL, EE when refracted went to F, it would be like ordinary refraction, which follows the ratio of sines, but [whereas] that for the ordinary refraction is approximately as 5 to 3 [1.666...], this is just under 8 to 5 [1.6], which is therefore less than the ordinary. The refracted rays are brought not to F, but to C, where the perpendicular AB is refracted to the bottom.
[As footnote 4 points out, this is only an approximation to what Huygens eventually determined: cf. Part VII, § 2 (p. 429).]
This kind of anomalous refraction is of rays in the plane perpendicular to the upper face at the line DE, which bisects the obtuse angle; but rays in other planes, erected in the same way from primary lines other than DE, are refracted less as the lines depart more from this plane of incidence, until if the plane cuts the line DE at right angles, the refraction of the rays of the plane is as 300 to 217, which is approximately 11 to 8. [In margin:] Or 10 to 7.
[p. 412]
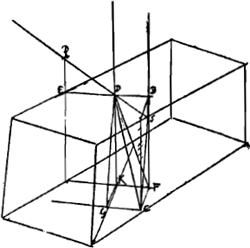
Fig. 134.
§ 5. See figure on page 5 [Fig. 134]. Given an arbitrary incident ray [PD], to obtain the plane that its refraction must follow, first imagine a plane [PDE] perpendicular to the surface at EDB. Then draw the line DG, which would be the refraction of a ray perpendicularly incident at the same place [D]. Then will be understood the plane DGCB through this line and through EDB. And for any ray incident in the perpendicular plane [PDE] through the surface, passing under the intersection with the surface, this [DGCB] will be the plane of refraction of the ray below the surface.
Hence I have understood the fact thus, as if an arbitrary incident ray [PD, as the editors note] were first carried by regular refraction but reached not the point that it ought to reach by that refraction (F in the figure) but another point C, under the line DE, at a distance from F determined by angle FBC or KDG, by which the anomalous refraction of the perpendicular recedes from the perpendicular. And this applies in general for rays incident on the surface in any plane.
So that the motion of the refracted ray within the crystal is composed, as it were, of the motion it would regularly have, and of a lateral motion whose quantity in the whole descent through the crystal is equal to the line FC. [This last paragraph is as translated by Dijksterhuis in, e.g., [5, p.149].]
* P.S. (27th October 2016)
The difference between the heights of the two images had been reported to the Royal Society in 1670, but without specifying the configuration or which image was higher [7, p.2043, par.10]. That report is apparently based on the treatise by Bartholinus [8], of which the relevant part is apparently “Experimentum IX”, which does not seem to deal with binocular vision or the location of an image using two lines of sight.**
In the above text, “principal plane” and “transverse plane” have been changed to “principal section” and “transverse section”.
** P.S. (2nd May 2017)
The text of Experiment IX in [8], as translated by Archibald, begins: “By thoroughly exerting the sense and keenness of the eyes, one of these two images may be seen to be higher than the other.” Note the plural eyes. Reading this under the influence of subsequent literature, one would think that Bartholinus was referring to the same phenomenon as Huygens. But the companion diagram shows only one eye and one viewpoint, uses highly oblique lines of sight to the two images, has nothing to do with binocular depth perception, and does not explain how far the lines of sight must be produced until they reach the apparent positions of the images. The subsequent Proposition IV, as translated by Archibald, states that “One image appears in a lower place than the other,” and does offer an explanation, albeit an unsatisfactory one: that the line of sight to the ordinary image (of an object on the far face of the crystal) is produced through a distance equal to the perpendicular thickness of the crystal, while the line of sight to the extraordinary image is produced through a distance equal to the thickness measured parallel to an edge of the crystal.
I cannot help noticing that if this construction is applied to a less oblique line of sight, it leads to the obviously and observably wrong conclusion that the extraordinary image is outside the crystal.
The corresponding experiment (numbered 17) in Bartholin's preliminary manuscript, as translated by Lohne [9, p.133] says: “When I looked attentively and carefully on the two images, one of them seemed more elevated than the other, the fixed image being uppermost. In our figure... If you imagine the [visual] rays of each image being produced from the eye...” Note the singular.
Bartholin's rule on how far to produce the lines of sight was apparently meant to follow (although it doesn't) from his inaccurate proposed law for the extraordinary refraction, namely that it satisfies Snell's law with the same index as the ordinary refraction, but with the angles referred to the edge instead of the normal. So, if he indeed beat Huygens in discovering the “two different stages” phenomenon, he was less eager to claim credit for that observation than to fit it to his theory!
References (updated 24 May 2018)
[1] Huygens (translated by S.P. Thompson), Treatise on Light, London: Macmillan, 1912; archive.org/details/treatiseonlight031310mbp. (See also G.R. Putland, “Errata in various editions of Huygens' Treatise on Light”, www.grputland.com or grputland.blogspot.com, 2016.)
[2] Newton, Opticks, 4th Ed. (London, 1730), Project Gutenberg, 2010, gutenberg.org/ebooks/33504. (The page number refers to the Gutenberg HTML edition.)
[3] J. Z. Buchwald, “Experimental investigations of double refraction from Huygens to Malus”, Archive for History of Exact Sciences, vol. 21, no. 4 (Dec. 1980), pp. 311–373.
[4] A.E. Shapiro, “Kinematic optics: A study of the wave theory of light in the seventeenth century”, Archive for History of Exact Sciences, vol. 11, no. 2/3 (June 1973), pp. 134–266.
[5] F.J. Dijksterhuis, Lenses and Waves: Christiaan Huygens and the Mathematical Science of Optics in the Seventeenth Century, Dordrecht: Kluwer Academic Publishers, 2004.
[6] Huygens, Oeuvres complètes, Tome XIX: Mécanique théorique et physique 1666–1695 (ed. J.A. Vollgraff), The Hague: Nijhoff, 1937, pp. 407–15, §§ 3–5 (and note 4 on p. 411).
[7] E. Bartholin (ed. H. Oldenburg?), “An Accompt of Sundry Experiments made and communicated by that Learn'd Mathematician, Dr. Erasmus Bartholin, upon a Chrystal-like Body, Sent to him out of Island”, Philosophical Transactions of the Royal Society, vol. 5, no. 67 (1670), pp. 2039–2048, rstl.royalsocietypublishing.org/content/5/57-68/2039.
[8] E. Bartholin, Experimenta Crystalli Islandici Disdiaclastici: Quibus mira et Insolita Refractio detegitur, Copenhagen (“Hafniæ”): D. Paulli, 1669, books.google.com/books?id=F7RAAAAAcAAJ (in Latin), translated by W. Brandt as Experiments with the Double Refracting Iceland Crystal: Which led to the discovery of a Marvelous and Strange Refraction, Westtown, Pa., 1959 (out of print). P.S. (7th November 2016): Also translated by T. Archibald as Experiments on Birefringent Icelandic Crystal, Copenhagen: Danish National Library of Science and Medicine, 1991 (also out of print).
[9] J.A. Lohne, “Nova experimenta crystalli Islandici disdiaclastici”, Centaurus, vol. 21, no. 2 (June 1977), pp. 106–148.
|
|
|